Kurvendiskussion - Aufgabe 4
Beispiel:
Untersuchen Sie die Funktion
$$f(x)=\frac{1}{2}x^3-4x^2+8x$$Lösung:
1. Ableitungen
\[\begin{array}{rl} f'(x)&=\frac{3}{2}x^2-8x+8\\ f''(x)&=3x-8\\ f'''(x)&=3 \end{array}\]2.Symmetrie des Graphen
Die Funktionsvorschrift f(x) besitzt gerade und ungerade Exponenten. Das bedeutet der Graph ist weder Punkt- noch Achsensymmetrisch.
3. Nullstellen
$$\color{purple}{\text{Nullstellen: } N_1(0|0),~N_2(4|0)}$$4. Extremstellen
$$\color{red}{\text{Extrempunkte: } H(1,33|4,74),T(4|0)}$$5. Wendestellen
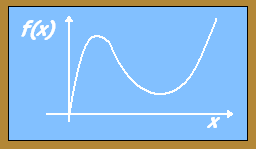
$$\color{blue}{\text{Wendestellen: } W(2,67|2,37)}$$6. Graph