Integralrechnen - Beispiel aus der Elektrotechnik
Gegeben ist der folgende Spannungsverlauf:
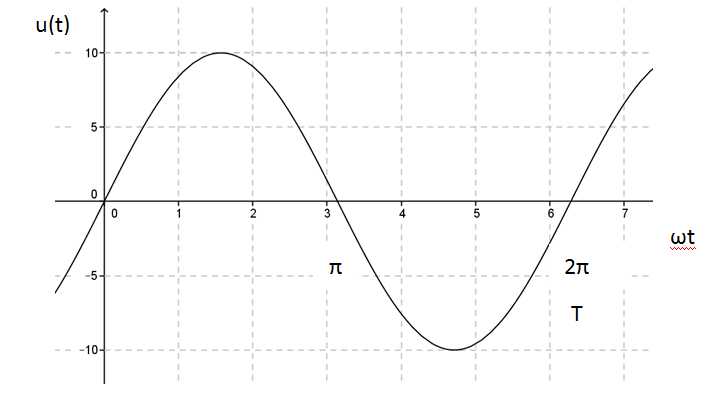
- Bestimmen Sie die Funktionsgleichung.
- Berechnen Sie den arithmetischen Mittelwert.
- Berechnen Sie den Effektivwert.
Lösung
Die Funktionsgleichung lautet: $$u(t)=10V \cdot sin(\omega t)$$
Der arithmetische Mittelwert berechnet sich wie folgt:
\[\begin{array}{rlll} U_{AV} &= &\frac{1}{T} &\int_0^T u(t)dt\\ U_{AV} &= &\frac{1}{T} &\int_0^T 10V sin(\omega t)dt\\ U_{AV} &= &\frac{10V}{T} &\int_0^T sin(\omega t)dt\\ \end{array}\] Die zu integrierende Funktion lautet: $$f(t)=sin(\omega t)$$ Dann ergibt sich für die Stammfunktion: $$F(t)=-\frac{1}{\omega} cos(\omega t)$$ Dieses Ergebnis können wir nun wieder in die Gleichung einsetzen: \[\begin{array}{rlll} U_{AV} &= &\frac{10V}{T} &(-\frac{1}{\omega}cos(\omega t))|_0^ T\\ U_{AV} &= &\frac{10V}{T} &(-\frac{1}{\omega}cos(\color{red}{\omega T})-(-\frac{1}{\omega}cos(\color{blue}{\omega \cdot 0}))) \end{array}\] Mit $$\color{red}{\omega T= 2\cdot \pi \cdot f \cdot \frac{1}{f}=2\cdot \pi}$$ und $$\color{blue}{\omega \cdot 0=0}$$ ergibt sich: \[\begin{array}{rlll} U_{AV} &= &\frac{10V}{T} &(-\frac{1}{\omega}cos(\color{red}{2\cdot \pi})-(-\frac{1}{\omega}cos(\color{blue}{0})))\\ U_{AV} &= &\frac{10V}{T} &(-\frac{1}{\omega}\cdot 1-(-\frac{1}{\omega}\cdot 1))\\ U_{AV} &= &\frac{10V}{T} &(-\frac{1}{\omega}+\frac{1}{\omega})\\ U_{AV} &= &\frac{10V}{T} &0\\ U_{AV} &= &0 \end{array}\]Der Effektivwert berechnet sich wie folgt:
$$U_{eff} = \sqrt{\frac{1}{T} \int_0^T u(t)^2 dt}$$ bzw. $$U_{eff}^2 = \frac{1}{T} \int_0^T u(t)^2 dt$$ Somit ergibt sich \[\begin{array}{rlll} U_{eff}^2 &= &\frac{1}{T} &\int_0^T (10V sin(\omega t))^2dt\\ U_{eff}^2 &= &\frac{1}{T} &\int_0^T (10V)^2 sin(\omega t)^2dt\\ U_{eff}^2 &= &\frac{100V^2}{T} &\int_0^T sin(\omega t)^2dt\\ \end{array}\] Die zu integrierende Funktion lautet: $$f(t)=sin(\omega t)^2$$ Es gilt aber auch $$sin(\omega t)^2=\frac{1}{2}-\frac{1}{2}cos(2\omega t)$$ somit folgt $$f(t)=\frac{1}{2}-\frac{1}{2}cos(2\omega t)$$ Dann ergibt sich für die Stammfunktion: $$F(t)=\frac{1}{2} t-\frac{1}{\omega} sin(\omega t)$$ Dieses Ergebnis können wir nun wieder in die Gleichung einsetzen: \[\begin{array}{rlll} U_{eff}^2 &= &\frac{100V^2}{T} &(\frac{1}{2} t-\frac{1}{\omega} sin(\omega t))|_0^ T\\ U_{eff}^2 &= &\frac{100V^2}{T} &(\frac{1}{2} T-\frac{1}{\omega} sin(\color{red}{\omega T})-(\frac{1}{2} 0-\frac{1}{\omega} sin(\color{blue}{\omega \cdot 0}))) \end{array}\] Mit $$\color{red}{\omega T= 2\cdot \pi \cdot f \cdot \frac{1}{f}=2\cdot \pi}$$ und $$\color{blue}{\omega \cdot 0=0}$$ ergibt sich: \[\begin{array}{rlll} U_{eff}^2 &= &\frac{100V^2}{T} &(\frac{1}{2} T-\frac{1}{\omega} sin(\color{red}{2\pi})-(\frac{1}{2} 0-\frac{1}{\omega} sin(\color{blue}{0})))\\ U_{eff}^2 &= &\frac{100V^2}{T} &(\frac{1}{2} T-0-0+0)\\ U_{eff}^2 &= &\frac{100V^2}{T} &\frac{1}{2} T\\ U_{eff}^2 &= &50V^2\\ U_{eff} &= &7,1V \end{array}\]
