Flächenberechnung - Beispiel 2
Betrachten wir die Flächen in den folgenden Bildern:
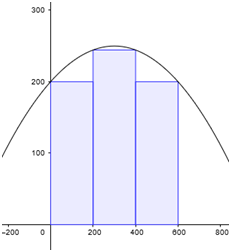
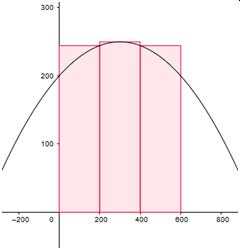
Die Breite der einzelnen Flächen berechnet sich durch die Gesamtbreite b geteilt durch die Anzahl der Flächen n.
$$(1)~~~\Delta x=\frac{b}{3}~\text{bzw. allgemein}~\Delta x=\frac{b}{n}$$
Die Höhe der einzelnen Flächen bestimmen wir durch den entsprechenden Funktionswert f(x).
Für die Gesamtfläche der Untersumme gilt:
$$\begin{array}{lll} A_{ges,U}&=A_1+A_2+A_3\\ &=f(0)\cdot\Delta x+f(\Delta x)\cdot\Delta x+f(2\Delta x)\cdot\Delta x\\ A_{ges,U}&=\Delta x\cdot (f(0)+f(\Delta x)+f(2\Delta x)) \end{array}$$
Um es übersichtlicher zu gestalten betrachten wir zunächst nur f(x)=x2
$$\begin{array}{lll} A_{ges,U}&=\Delta x\cdot ( 0^2+(\Delta x)^2 + (2\Delta x)^2)\\ &=\Delta x\cdot ( 0^2+(\Delta x)^2 + 4(\Delta x)^2)\\ A_{ges,U}&=(\Delta x)^3\cdot ( 0+1+4) \end{array}$$
Betrachten wir nun nicht nur 3 Flächen sondern vergrößern die Anzahl der Flächen auf n, dann ergibt sich
$$A_{ges,U}=(\Delta x)^3\cdot ( 0+1+4\color{blue}+9+16+\dots+(n-1)^2)$$
bzw. mit (1)
$$A_{ges,U}=(\frac{b}{n})^3\cdot ( 0+1+4\color{blue}{+9+16+\dots+(n-1)^2)}$$
Gleiches wiederholen wir nun für die Gesamtfläche der Obersumme:
Dieser Quader ist für n=3 n-Einheiten hoch, (2n+1) Einheiten breit und (n+1) Einheiten tief. Also gilt für
$$(1+4+9) = \frac{n(n+1)(2n+1)}{6}$$Und somit für die Obersumme ebenfalls:
$$(1+4+9\color{red}+16+\dots+n^2) = \frac{n(n+1)(2n+1)}{6}$$Klammern wir n aus jeder Klammer aus, ergibt sich
$$\frac{n(n+1)(2n+1)}{6}=\frac{n\cdot n(1+\frac{1}{n})n(2+\frac{1}{n})}{6}=\color{red}\frac{n^3\cdot (1+\frac{1}{n})(2+\frac{1}{n})}{6}\color{black}$$ $$ \begin{array}{rl} A_{ges,O}&=A_1+A_2+A_3\\ &=f(\Delta x)\cdot\Delta x+f(2\Delta x)\cdot\Delta x +f(3\Delta x)\cdot\Delta x\\ A_{ges,O}&=\Delta x\cdot (f(\Delta x)+f(2\Delta x)++f(3\Delta x)) \end{array} $$ Wir betrachten wieder nur f(x)=x2: $$\begin{array}{rl} A_{ges,O}&=\Delta x\cdot ((\Delta x)^2 + (2\Delta x)^2+ (3\Delta x)^2)\\ &=\Delta x\cdot ( (\Delta x)^2 + 4(\Delta x)^2)+ 9(\Delta x)^2)\\ A_{ges,O}&=(\Delta x)^3\cdot (1+4+9) \end{array} $$Allgemein ergibt sich auch hier
$$A_{ges,O}=(\Delta x)^3\cdot ( 1+4+9\color{red}{+16+\dots+n^2})$$ bzw. mit (1) $$A_{ges,O}=(\frac{b}{n})^3\cdot ( 1+4+9+\color{red}{16+\dots+n^2}) $$Mit den Formeln (4) und (5) (die Herleitung finden Sie hier)
$$(4)~~~(0+1+4\color{blue}+9+16+\dots+(n-1)^2)=\color{blue}\frac{n^3\cdot (1-\frac{1}{n})(2-\frac{1}{n})}{6}\color{black}$$ $$(5)~~~(1+4+9\color{red}+16+\dots+n^2)=\color{red}\frac{n^3\cdot (1+\frac{1}{n})(2+\frac{1}{n})}{6}\color{black}$$und der Tatsache, dass der Flächeninhalt zwischen den Flächen von Ober- und Untersumme liegt, folgt
$$ \begin{array}{rl} A_{ges,U} &\leq A_{ges}\leq A_{ges,O}\\ \frac{b^3}{n^3}\cdot\frac{n^3\cdot (1-\frac{1}{n})(2-\frac{1}{n})}{6} &\leq A_{ges}\leq \frac{b^3}{n^3}\cdot\frac{n^3\cdot (1+\frac{1}{n})(2+\frac{1}{n})}{6}\\ \frac{b^3\cdot(1-\frac{1}{n})(2-\frac{1}{n})}{6} &\leq A_{ges}\leq \frac{b^3\cdot(1+\frac{1}{n})(2+\frac{1}{n})}{6} \end{array} $$Erhöhen wir nun die Anzahl der Rechtecke n →∞ ergibt sich
$$\begin{array}{rl} \frac{b^3\cdot1\cdot 2}{6} &\leq A_{ges}\leq \frac{b^3\cdot 1\cdot 2}{6}\\ \frac{b^3}{3} &\leq A_{ges}\leq \frac{b^3}{3} \end{array}$$Betrachten wir die Summe der Quadrate einmal geometrisch. Dann können wir für die Summe (1+4+9) den folgenden Quader konstruieren:
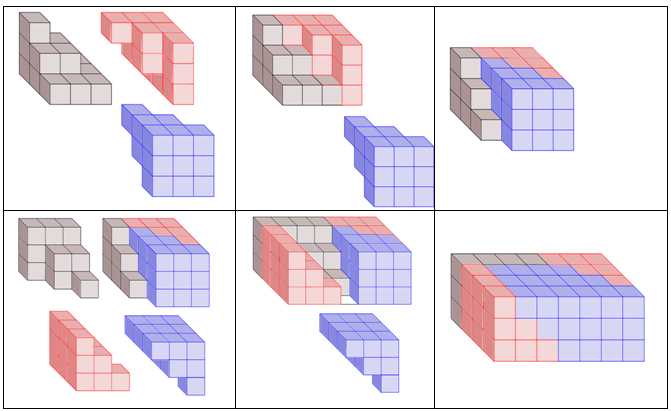
Dieser Quader ist für n=3 n-Einheiten hoch, (2n+1) Einheiten breit und (n+1) Einheiten tief. Also gilt für
$$(1+4+9) = \frac{n(n+1)(2n+1)}{6}$$Und somit für die Obersumme ebenfalls:
$$(1+4+9\color{red}+16+\dots+n^2) = \frac{n(n+1)(2n+1)}{6}$$Klammern wir n aus jeder Klammer aus, ergibt sich
$$(4)~~~\frac{n(n+1)(2n+1)}{6}=\frac{n\cdot n(1+\frac{1}{n})n(2+\frac{1}{n})}{6}=\color{red}{\frac{n^3\cdot (1+\frac{1}{n})(2+\frac{1}{n})}{6}}$$Für die Untersumme müssen wir anstelle von n den Term (n-1) einsetzen. Dann ergibt sich:
\begin{array}{lr} (0+1+4\color{blue}+9+16+\dots+(n-1)^2) &= \frac{(n-1)(n-1+1)(2(n-1)+1)}{6}\\ &=\frac{(n-1)(n)(2n-2+1)}{6}\\ &=\frac{(n-1)n(2n-1)}{6} \end{array}Auch hier klammern wir aus:
$$(5)~~~\frac{n(n-1)(2n-1)}{6}=\frac{n\cdot n(1-\frac{1}{n})n(2-\frac{1}{n})}{6}=\color{blue}{\frac{n^3\cdot (1-\frac{1}{n})(2-\frac{1}{n})}{6}}$$ Zurück
