Flächenberechnung - Beispiel 5
| Berechnen Sie die Fläche zwischen den Graphen \(f(x)=-x^2+6x-4\) und \(g(x)=x^2-4x+4\) zwischen den Schnittpunkten. | 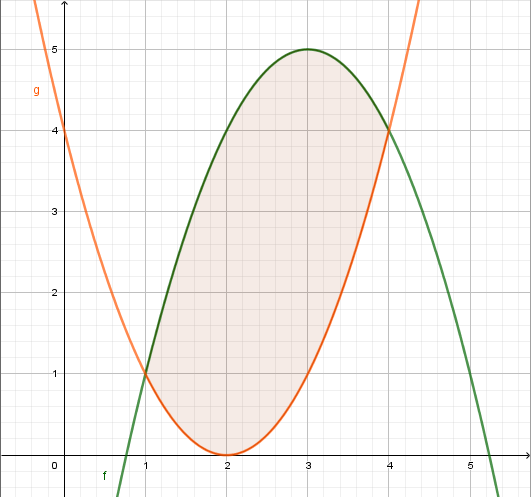 |
Lösung:
| Wir berechnen zunächst die Fläche \(A_1\) unterhalb von f(x). | 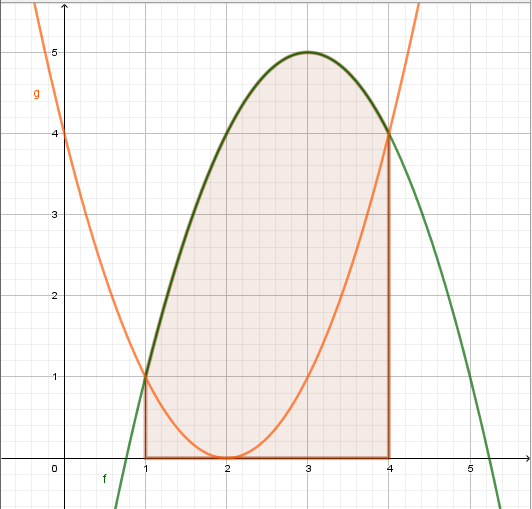 |
| Anschließend die Fläche \(A_2\) unterhalb von g(x). | 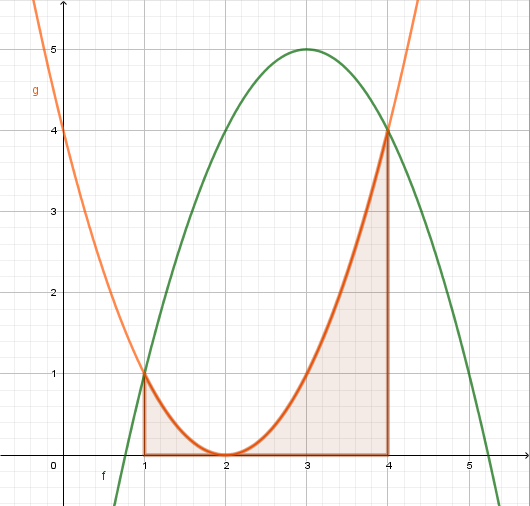 |
| Im dritten Schritt berechnen wir die Gesamtfläche, indem wir die anderen beiden Flächen voneinander abziehen.$$ A_{ges}=A_1-A_2$$ |
Die Integrationsgrenzen bestimmen wir, indem wir die Schnittpunkte der Funktionen berechnen:
$$\begin{array}{rlll} f(x) &&= &&g(x)\\ -x^2+6x-4 &&=&&x^2-4x+4&& | +x^2\\ 6x-4 &&=&&2x^2-4x+4&& | -6x\\ -4 &&=&&2x^2-10x+4&& | +4\\ 0&&=&&2x^2-10x+8&& | :2\\ 0&&=&&x^2-5x+4&& \end{array}$$
Anwenden der pq-Formel ergibt:
$$x_{1,2}=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$$
Mit \(p=-5\) und \(q=4\) folgt
$$\begin{array}{rlll} x_{1,2} &&= & &-\frac{-5}{2}\pm\sqrt{\left(\frac{-5}{2}\right)^2-4}\\ x_{1,2} &&= && 2,5\pm\sqrt{6,25-4}\\ x_{1,2} &&= && 2,5\pm 1,5\\ x_1 &&= &&4\\ x_2 &&= &&1 \end{array}$$
Nun können wir die einzelnen Flächen berechnen:
$$f(x)=-x^2+6x-4$$
$$F(x)=-\frac{1}{3}x^3+3x^2-4x$$
$$\begin{array}{lll} A_1 &&= &&\int_1^4 f(x)dx\\ &&= &&[F(x)]_1^4\\ &&= && F(4)-F(1)\\ &&= && -\frac{1}{3}\cdot 4^3+3\cdot 4^2-4\cdot 4-(-\frac{1}{3}\cdot 1^3+3\cdot 1^2-4\cdot 1)\\ &&= && 10,7 + 1,33\\ &&= && 12 \end{array}$$
$$g(x)=x^2-4x+4$$
$$G(x)=\frac{1}{3}x^3-2x^2+4x$$
$$\begin{array}{lll} A_2 &&= &&\int_1^4 f(x)dx\\ &&= &&[G(x)]_1^4\\ &&= && G(4)-G(1)\\ &&= && \frac{1}{3}\cdot 4^3-2\cdot 4^2+4\cdot 4-(\frac{1}{3}\cdot 1^3-2\cdot 1^2+4\cdot 1x)\\ &&= && 5,33 - 2,33\\ &&= && 3 \end{array}$$
Damit ergibt sich für die Gesamtfläche:
$$\begin{array}{lll} A_{ges} &&= &&A_1-A_2\\ &&= &&12-3\\ A_{ges} &&= &&9 \end{array}$$

