Flächenberechnung - Beispiel 4
| Berechnen Sie die Fläche zwischen dem Graphen der Funktion und der x-Achse im Intervall \([0|4]\). Berechnen Sie dazu zuerst die Integrationsgrenzen.$$f(x)=-x^2+4x-3$$ | 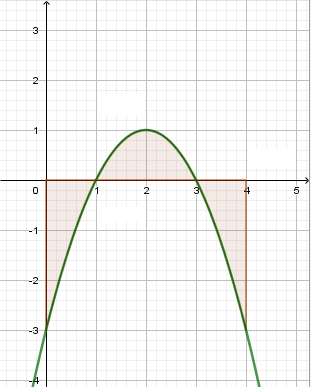 |
Lösung:
Zuerst bestimmen wir die Integrationsgrenzen, d.h. wir suchen die Nullstellen der Funktion:
$$f(x)=0$$
$$\begin{array}{rlll} 0 &&=&&-x^2+4x-3&& |\cdot (-1)\\ 0 &&=&&x^2-4x+3&& \end{array}$$
Nun können wir die pq-Formel anwenden:
$$x_{1,2}=-\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q}$$
Mit \(p=-4\) und \(q=3\) folgt
$$\begin{array}{rlll} x_{1,2} &&= & &-\frac{-4}{2}\pm\sqrt{\left(\frac{-4}{2}\right)^2-3}\\ x_{1,2} &&= && 2\pm\sqrt{4-3}\\ x_{1,2} &&= && 2\pm 1\\ x_1 &&= &&3\\ x_2 &&= &&1 \end{array}$$
Nun können wir die einzelnen Flächen berechnen. Dazu bilden wir zunächst die Stammfunktion:
$$f(x)=-x^2+4x-3$$
$$F(x)=-\frac{1}{3}x^3+2x^2-3x$$
$$\begin{array}{lll} A_1 &&= &&\int_0^1f(x)dx\\ &&= &&\int_0^1-x^2+4x-3dx\\ &&= &&[F(x)]_0^1\\ &&= &&[-\frac{1}{3}x^3+2x^2-3x]^1_0\\ &&= && F(1)-F(0)\\ &&= && -\frac{1}{3}\cdot 1^3+2\cdot1^2-3\cdot 1-(-\frac{1}{3}\cdot 0^3+2\cdot 0^2-3\cdot 0)\\ &&= && -\frac{4}{3} - (0)\\ &&= && -1,33 \end{array}$$
Durch das negative Vorzeichen wird deutlich, dass sich die Fläche \(A_1\) unterhalb der x-Achse befindet.
$$\begin{array}{lll} A_2 &&= &&\int_1^3f(x)dx\\ &&= &&\int_1^3-x^2+4x-3dx\\ &&= &&[F(x)]_1^3\\ &&= &&[-\frac{1}{3}x^3+2x^2-3x]^3_1\\ &&= && F(3)-F(1)\\ &&= && -\frac{1}{3}\cdot 3^3+2\cdot 3^2-3\cdot 3-(-\frac{1}{3}\cdot 1^3+2\cdot 1^2-3\cdot 1)\\ &&= && -9 +18 -9 -(-\frac{4}{3})\\ &&= && 0+\frac{4}{3}\\ &&= && 1,33 \end{array}$$
\(A_2\) befindet sich oberhalb der x-Achse.
$$\begin{array}{lll} A_3 &&= &&\int_3^4f(x)dx\\ &&= &&\int_3^4-x^2+4x-3dx\\ &&= &&[F(x)]_3^4\\ &&= &&[-\frac{1}{3}x^3+2x^2-3x]^4_3\\ &&= && F(4)-F(3)\\ &&= && -\frac{1}{3}\cdot 4^3+2\cdot 4^2-3\cdot 4-(-\frac{1}{3}\cdot 3^3+2\cdot 3^2-3\cdot 3)\\ &&= && -21\frac{1}{3}+32-12 -(0)\\ &&= && -\frac{4}{3}\\ &&= && -1,33 \end{array}$$
\(A_3\) befindet sich wieder unterhalb der x-Achse.
Für die Gesamtfläche ergibt sich dann:
$$\begin{array}{lll} A_{ges} &&= &&A_1+A_2+A_3\\ &&= &&1,33+1,33+1,33\\ &&= && 4 \end{array}$$

