Kurvendiskussion - Aufgabe 3
Beispiel:
Untersuchen Sie die Funktion
$$f(x)=x^5-5x^4+6,25x^3$$Lösung:
1. Ableitungen
\[\begin{array}{rl} f'(x)&=5x^4-20x^3+18,75x^2\\ f''(x)&=20x^3-60x^2+37,5x\\ f'''(x)&=60x^2-120x+37,5 \end{array}\]2.Symmetrie des Graphen
Die Funktionsvorschrift f(x) besitzt gerade und ungerade Exponenten. Das bedeutet der Graph ist weder Punkt- noch Achsensymmetrisch.
3. Nullstellen
\[\begin{array}{rll} f(x) &=0&\\ 0 &=x^5-5x^4+6,25x^3 &\text{ ausklammern}\\ 0 &=x^3(x^2-5x+6,25)&| \end{array}\]Also ergibt sich als 1. Nullstelle:
\[\begin{array}{rll} x^3 &=0&|\sqrt[3]{}\\ x &=0 \end{array}\]Nun untersuchen wir die Teilfunktion
$$x^2-5x+6,25=0$$Die weiteren Nullstellen finden wir mithilfe der pq-Formel. Mit p=-5 und q=6,25 ergibt sich:
\[\begin{array}{rll} x_{2,3} &=-\frac{p}{2}\pm\sqrt{(-\frac{p}{2})^2-q}&\\ x_{2,3} &=-\frac{-5}{2}\pm\sqrt{(-\frac{-5}{2})^2-6,25}&\\ x_{2,3} &=2,5\pm\sqrt{6,25-6,25}&\\ x_{2,3} &=2,5\pm\sqrt{0}&\\ x_{2,3} &=2,5&\\ \end{array}\]Also besitzt die Gleichung f(x)=0 folgende Lösungen:
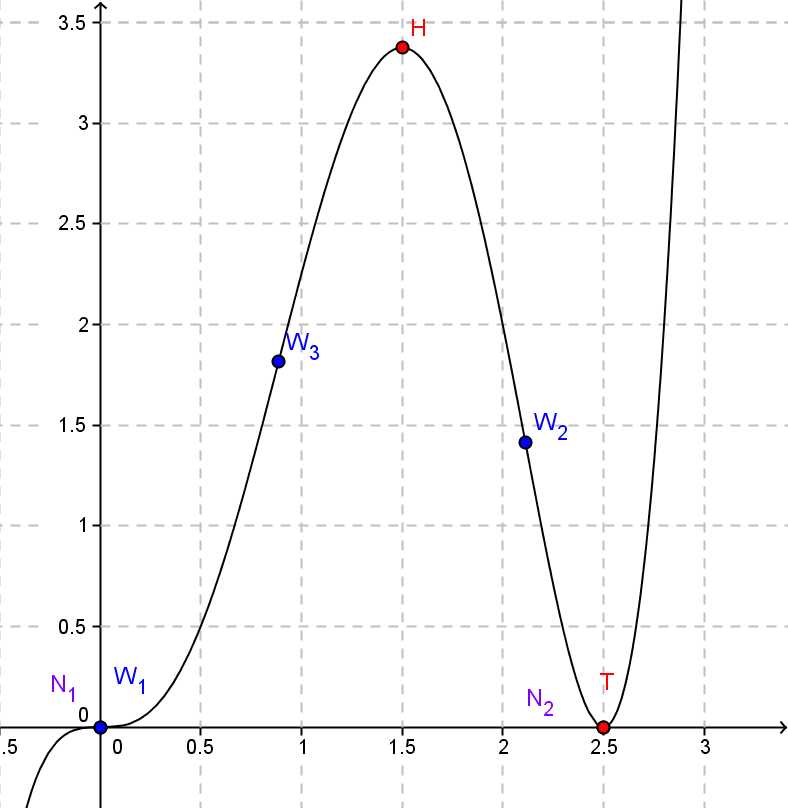
$$x_1=0, x_2=2,5$$ $$\color{purple}{\text{Nullstellen: } N_1(0|0),~N_2(2,5|0)}$$4. Extremstellen
\[\begin{array}{rl} f'(x) &= 0\\ 5x^4-20x^3+18,75x^2 &=0\\ 5x^2(x^2-4x+3,75) &=0\\ \end{array}\]Also ergibt sich als möglicher Extremwert:
\[\begin{array}{rll} 5x^2 &=0&|:5\\ x^2 &=0&|\sqrt{}\\ x_3&=0& \end{array}\]Nun untersuchen wir die Teilfunktion
$$x^2-4x+3,75=0$$Mithilfe der pq-Formel und p=-4 und q=3,75 ergibt sich:
\[\begin{array}{rll} x_{4,5} &=-\frac{p}{2}\pm\sqrt{-\frac{p}{2}^2-q}&\\ x_{4,5} &=-\frac{-4}{2}\pm\sqrt{-(\frac{-4}{2})^2-3,75}&\\ x_{4,5} &=2\pm\sqrt{4-3,75}&\\ x_{4,5} &=2\pm\sqrt{0,25}&\\ x_{4,5} &=2&\pm 0,5\\ x_4&=2,5&\\ x_5&=1,5& \end{array}\]Nun überprüfen wir, ob es sich bei den gefundenen Nullstellen der Steigungsfuktion um Extremwerte handelt. Dazu verwenden wir die 2. Ableitung
$$f''(x)=20x^3-60x^2+37,5x$$Für \(x_3=0\) ergibt sich
$$f'(0)=0,~f''(0)=0$$Hierbei handelt es sich um keine Extremstelle. (\(f'''(x)=37,5>0\), ungerade Ableitung, also Wendestelle)
Für \(x_4=2,5\) ergibt sich
$$f'(2,5)=0,~f''(2,5)=20\cdot (2,5)^3-60\cdot(2,5)^2+37,5\cdot(2,5)=31,25>0$$ein lokales Minimum.
Für \(x_4=1,5\) ergibt sich
$$f'(1,5)=0,~f''(1,5)=20\cdot (1,5)^3-60\cdot(1,5)^2+37,5\cdot(1,5)=-11.25<0$$ein lokales Maximum.
Eingesetzt in f(x) ergibt sich:
$$\color{red}{\text{Extrempunkte: } T(2,5|0),H(1.5|3.38)}$$5. Wendestellen
\[\begin{array}{rl} f''(x) &= 0\\ 20x^3-60x^2+37,5x &=0\\ 20x(x^2-3x+1,875)&=0 \end{array}\]Also ergibt sich als mögliche Wendestelle:
\[\begin{array}{rll} 20x &=0&|:20\\ x_7&=0& \end{array}\]Nun untersuchen wir die Teilfunktion
$$x^2-3x+1,875=0$$Mithilfe der pq-Formel und p=-3 und q=1,875 ergibt sich:
\[\begin{array}{rll} x_{8,9} &=-\frac{p}{2}\pm\sqrt{-\frac{p}{2}^2-q}&\\ x_{8,9} &=-\frac{-3}{2}\pm\sqrt{-(\frac{-3}{2})^2-1,875}&\\ x_{8,9} &=1,5\pm\sqrt{2,25-1,875}&\\ x_{8,9} &=1,5\pm\sqrt{0,375}&\\ x_{8,9} &=1,5&\pm 0,612\\ x_8&=2,12&\\ x_9&=0,888& \end{array}\]Nun überprüfen wir, ob es sich bei den gefundenen Nullstellen der 2.Ableitung um Wendestellen handelt. Dazu verwenden wir die 3. Ableitung
$$f'''(x)=60x^2-120x+37,5$$Für \(x_7=0\) ergibt sich
$$f''(0)=0,~f'''(0)=37,5>0$$Hierbei handelt es sich um einen Wendepunkt, bzw. Sattelpunkt, da f'(0)=0
Für \(x_8=2,12\) und \(x_9=0,88\) ergeben sich
$$f''(2,12)=0,~f'''(2,12)=51,4>0$$ $$f''(0,88)=0,~f'''(0,88)=21,6>0$$weiter Wendestellen.
Jeweils eingesetzt in f(x) folgt
\[\begin{array}{rll} f(0)&=0&\\ f(2,12)&=1,38&\\ f(0,88)&=1,79 \end{array}\]Somit ergeben sich die folgenden Wendestellen:
$$\color{blue}{\text{Wendestellen: } W_1(0|0),~W_2(0,88|1,79),~W_3(2,12|1.38)}$$6. Graph