1. Ableitungen

\[\begin{array}{rl} f'(x)&=4x^3-8x\\ f''(x)&=12x^2-8\\ f'''(x)&=24x \end{array}\]

2.Symmetrie des Graphen

Die Funktionsvorschrift f(x) besitzt ausschließlich gerade Exponenten. Das bedeutet der Graph ist symmetrisch zur y-Achse

3. Nullstellen

\[\begin{array}{rll} f(x) &=0&\\ 0 &=x^4-4x^2&|x^2 \text{ ausklammern}\\ 0 &=x^2(x^2-4)&|\text{3. binomische Formel} \\ 0 &=x^2(x+2)(x-2)& \end{array}\] Also besitzt die Gleichung f(x)=0 folgende Lösungen: $$x_1=0,~ x_2=-2, x_3=2$$ $$\color{purple}{\text{Nullstellen: } N_1(-2|0),~N_2(0|0),~N_3(2|0)}$$

4. Extremstellen

\[\begin{array}{rl} f'(x) &= 0\\ 4x^3-8x &=0\\ x(4x^2-8) &=0\\ x(2x+\sqrt{8})(2x-\sqrt{8})=0 \end{array}\] Also besitzt die Gleichung f'(x)=0 folgende Lösungen: $$x_4=0,~ x_5=-\sqrt{2}, x_6=\sqrt{2}$$ Für $$x_4=0$$ ergibt sich $$f'(0)=0,~f''(0)=-8\leq0$$ ein lokales Maximum. Für $$x_5=-\sqrt{2}$$ ergibt sich $$f'(-\sqrt{2})=0,~f''(-\sqrt{2})=16>0$$ ein lokales Minimum. Für $$x_6=\sqrt{2}$$ ergibt sich $$f'(\sqrt{2})=0,~f''(\sqrt{2})=16>0$$ ebenfalls ein lokales Minimum. $$\color{red}{\text{Extrempunkte: } T_1(-1,41|-4),H(0|0),~T_2(1,41|-4)}$$

5. Wendestellen

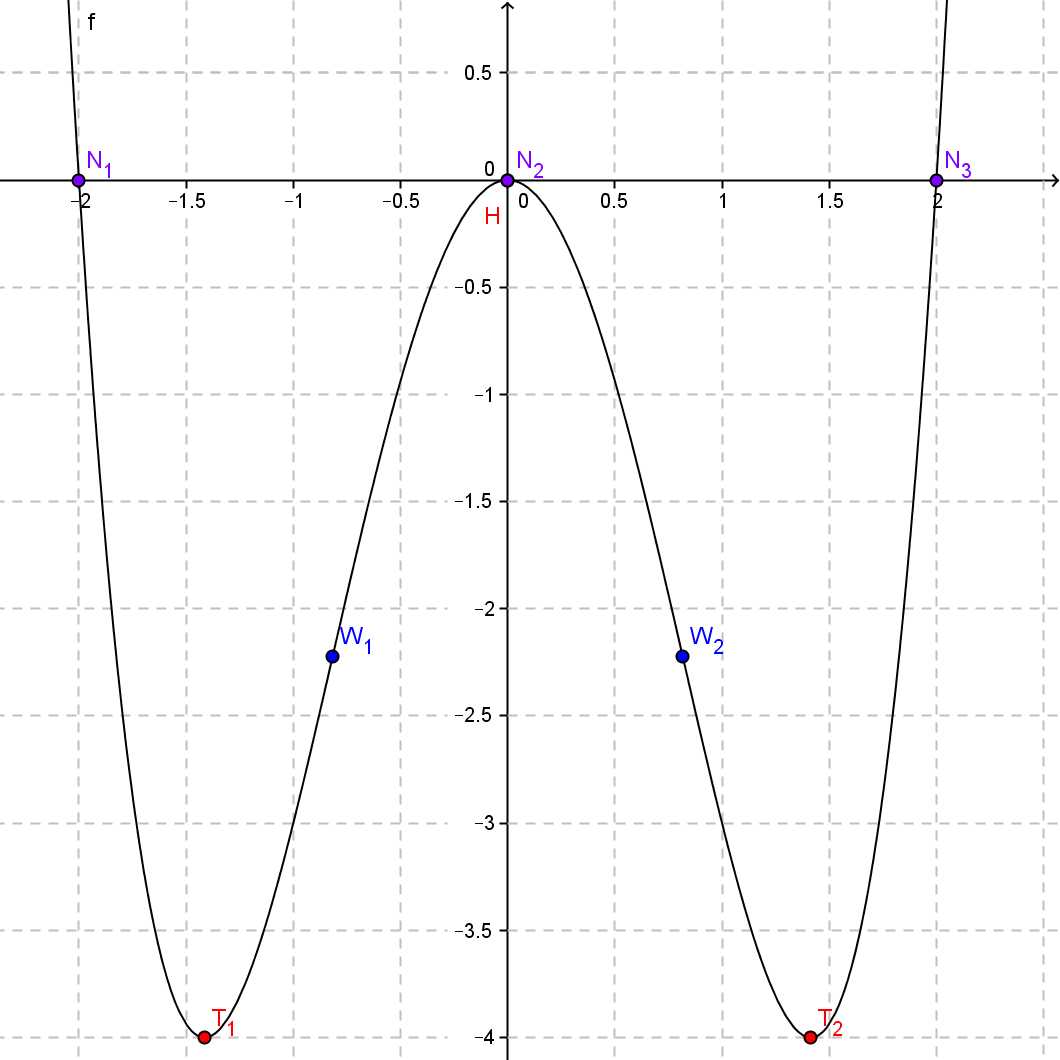
\[\begin{array}{rl} f''(x) &= 0\\ 12x^2-8 &=0\\ (\sqrt{12}x+\sqrt{8})(\sqrt{12}x-\sqrt{8})&=0 \end{array}\] Also besitzt die Gleichung f''(x)=0 folgende Lösungen: $$x_7=-0,816,~ x_8=0,816$$ Für $$x_7=-0,816$$ ergibt sich $$f'''(-0,816)=-19,59\neq 0$$ eine Wendestelle. Für $$x_8=0,816$$ ergibt sich $$f'''(0,816)=19,59\neq 0$$ eine weitere Wendestelle. $$\color{blue}{\text{Wendestellen: } W_1(-0,816|-2,22),~W_2(0,816|-2,22)}$$